Studying ultrafast physical processes that unfold on femtosecond and attosecond timescales necessitates laser sources capable of generating ultrashort pulses. These pulses should not only possess high peak power but also have precisely controllable electric fields. For applications where precise control over the generated light field is paramount, maintaining a stable carrier-envelope phase (CEP) is crucial. At present, various techniques are available for compressing few-cycle pulses with millijoule-level energy. These techniques encompass the use of gas-filled hollow-core fibers (HCFs) and multipass cavities (MPCs), among others. Nevertheless, these systems frequently fall short in simultaneously achieving CEP stability and flexible repetition rate tunability. To cater to diverse repetition rate requirements, this paper introduces a high-repetition-rate laser system. This system is not only tunable in repetition rate but also maintains CEP stability, all while preserving excellent beam quality[1].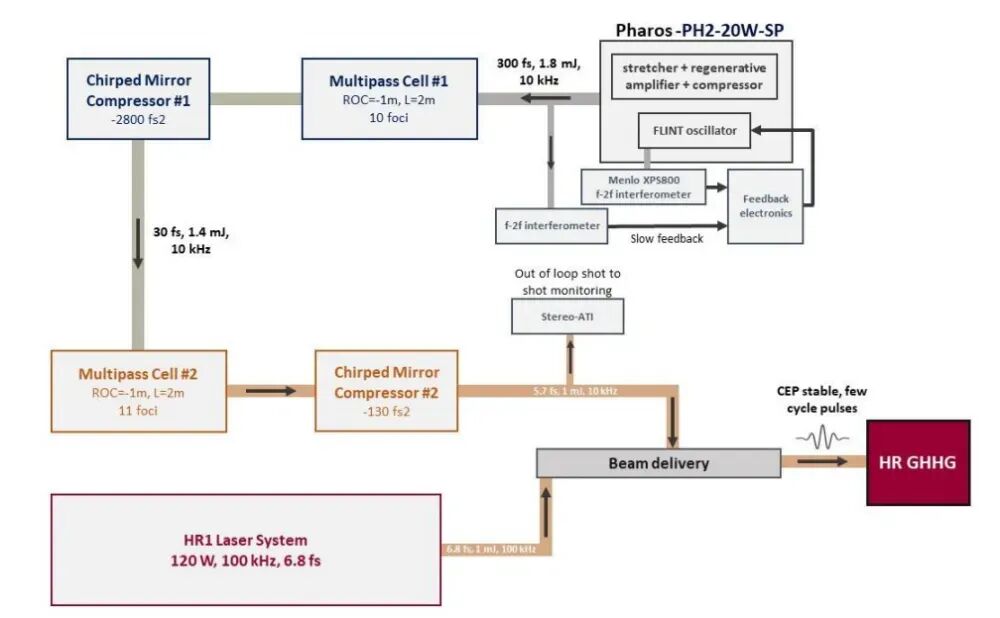

Figure 1. Overall Optical Layout[1]

Figure 1 showcases the overall optical layout of the experimental setup. The front end of the device is equipped with a Pharos-PH2-20W-SP laser. This laser delivers CEP-stable pulses with a duration of 300 fs at a wavelength of 1030 nm. It boasts an average power of 20 W and an adjustable repetition rate that can reach up to 1 MHz. Following the laser, two f-2f interferometers are employed to establish a CEP stabilization feedback loop. The first f-2f interferometer directly stabilizes the carrier-envelope offset frequency of the oscillator. Meanwhile, the second interferometer measures the relative CEP of the output and provides feedback to the oscillator. This feedback mechanism is crucial for stabilizing long-term CEP drift. The setup utilizes a two-stage MPC compression scheme. In the first stage, a multipass cavity with a length of 2 m and mirrors having a 1 m radius of curvature is used. The focus passes through this cavity 10 times in the presence of 0.6 bar of krypton gas. After undergoing spectral broadening, the pulses are compressed using chirped mirrors. These mirrors compensate for a group delay dispersion (GDD) of -2800 fs². As a result, the first-stage MPC compresses the 300 fs pulses down to 30 fs. During this process, the pulse energy decreases from 1.8 mJ to 1.4 mJ. The second-stage MPC shares the same cavity length and mirrors as the first stage. Here, the focus passes through the cavity 11 times in the presence of 0.15 bar of argon gas. The compressor again employs chirped mirrors, this time providing a GDD of -248 fs² and a third-order dispersion of -247 fs³. The second-stage MPC further compresses the pulses to a mere 5.7 fs, with the pulse energy decreasing from 1.4 mJ to 1.1 mJ. Subsequently, 10% of the output light energy is diverted for Stereo-ATI sampling. To counteract the dispersion introduced by the diverted optical path, chirped mirrors are used once more. These mirrors provide a GDD of -134 fs². The remaining output light then enters the beam delivery system. In this system, it can serve as alignment light for the HR1 laser system or directly function as the primary laser for experiments, such as high-order harmonic generation. The output beam is nearly diffraction-limited, with M² values of 1.00 and 1.16 along the x-axis and y-axis, respectively. The ellipticity of the output beam is maintained between 0.94 and 1.00, with astigmatism at a mere 0.04% of the focal length. Figure 2 presents the results of measuring the temporal profile of the output pulses using a d-scan device. The transform-limited pulse duration is 5.7 fs, with the main peak pulse containing 86.3% of the pulse energy. Figure 3(d) also displays the measured pulse durations at different repetition rates. This demonstrates that the laser pulses are independent of the repetition rate, maintaining durations consistently at 5.7 ± 0.1 fs.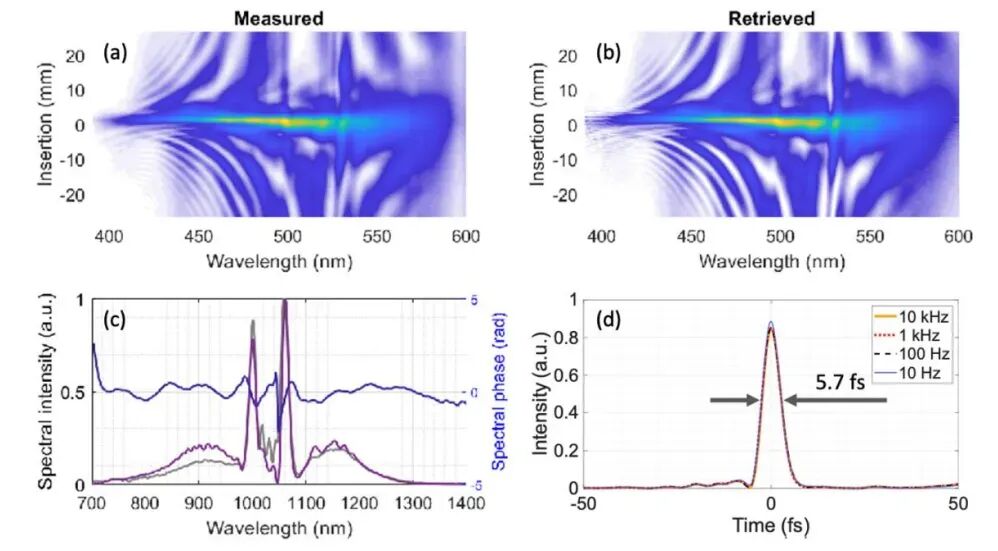

Figure 2. (a) Measured and (b) retrieved d-scan traces of the output waveform; (c) measured (gray) and retrieved (purple) spectra; (d) reconstructed temporal shapes of the output pulses at different repetition rates[1]

Figure 3 shows the third-order autocorrelation curve of the output pulses, spanning a time scale from -500 ps to 500 ps. The relative intensity on the prepulse side drops below 10⁻⁶ at -2 ps. Overall, the ASE contrast can reach the 10⁻¹⁰ level. However, some prepulses on the order of 10⁻⁵ still persist, warranting further investigation.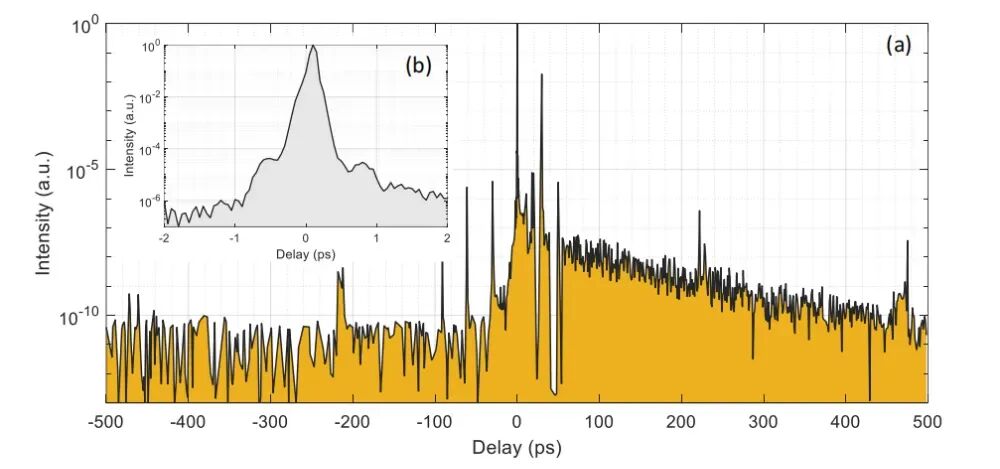

Figure 3. (a) Third-order autocorrelation curve of the output pulses; (b) Enlarged view from -2 ps to 2 ps[1]

Figure 4 illustrates the spectral evolution of the laser pulses. The first-stage MPC broadens the spectral width from 10.2 nm to 82.5 nm. Subsequently, the second-stage MPC further expands it to 408.1 nm, achieving an overall broadening factor exceeding 40 times.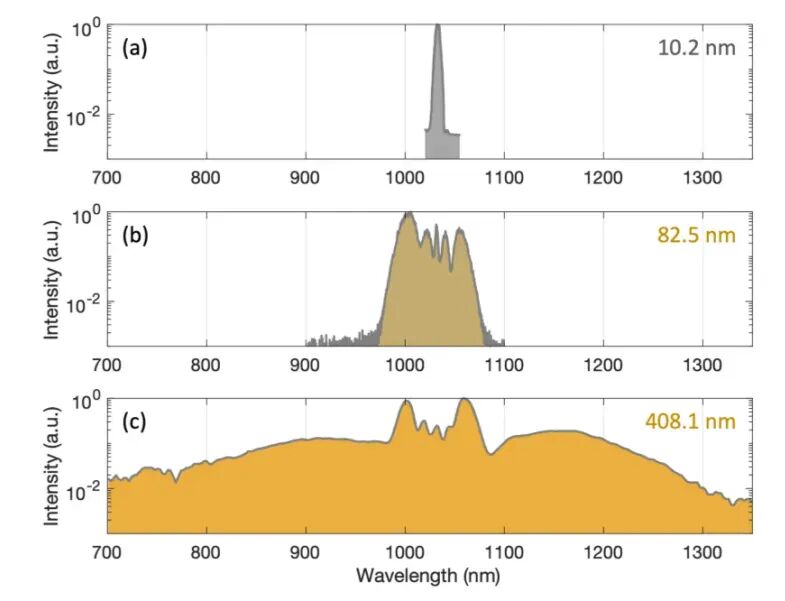

Figure 4. Spectral evolution of the pulses from the front end (a) to after the first-stage MPC (b) and then to the back end (c)[1]

Figure 5 also depicts the time-dependent variation in the photoelectron and photoion particle count rates generated by the single ionization of argon under extreme ultraviolet light irradiation. These rates remain stable over an 8-hour experiment. Additionally, the root mean square (RMS) fluctuation in output pulse energy stability was measured to be less than 0.04% over a 1-hour period.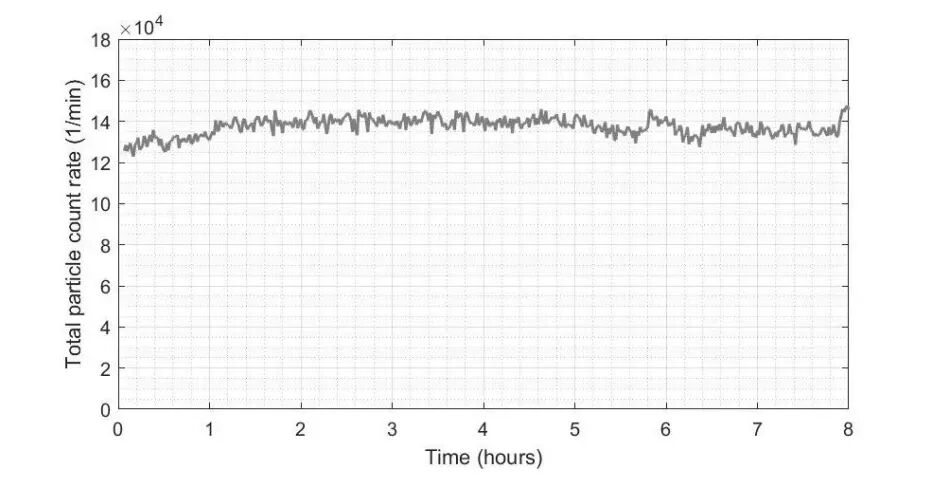

Figure 5. Time-dependent variation in the photoelectron and photoion particle count rates generated by single-photon excitation[1]

In conclusion, this paper presents a compact, high-repetition-rate laser system. This system is not only tunable in repetition rate but also maintains CEP stability. It is capable of delivering pulses with widths less than 6 fs and energies exceeding 1 mJ, making it suitable for driving high-order harmonic generation and attosecond spectroscopy. The system demonstrates exceptional performance in terms of energy stability, beam quality, and temporal contrast, with all parameters pushed to their limits.

References: [1] Gilicze B, Seres I, Bengery Z, et al. Repetition-rate-independent post-compression to achieve CEP stable few-cycle laser pulses. High Power Laser Science and Engineering. Published online 2025:1-20. doi:10.1017/hpl.2025.10081