In the realm of ultrafast laser systems, achieving high-precision time-resolved applications necessitates compressing laser pulses to the few-cycle level or even below 10 fs. Traditional pulse compression methods often rely on dispersion compensation elements, such as chirped mirrors, grating pairs, hollow-core fibers, or transparent solid materials. While these techniques are effective, they entail complex setups, large system sizes, and stringent requirements for alignment precision and environmental stability.

Researchers have devised a novel method for femtosecond pulse self-compression utilizing conical radiation in normal-pressure air. This method successfully compresses initial 98 fs near-infrared laser pulses to 8.8 fs without the need for additional dispersion compensation structures [1].

The experimental setup is illustrated in Figure 1. It primarily comprises three components: a focusing lens to generate air plasma and conical radiation, a concave silver mirror to re-collimate the conical beam, and a spatial aperture with a 4 mm diameter to select the compressed pulse region. The compressed pulse then enters the SHG-FROG system for pulse width measurement, while its spectral characteristics are analyzed using a grating spectrometer. The experiment employs a titanium sapphire laser emitting 98 fs pulses with a central wavelength of 804 nm and a single pulse energy of 1.8 mJ. The laser beam is focused into normal-pressure air through a fused silica convex lens with a focal length of 150 mm. During focusing, the laser pulse experiences spectral broadening due to self-phase modulation (SPM).

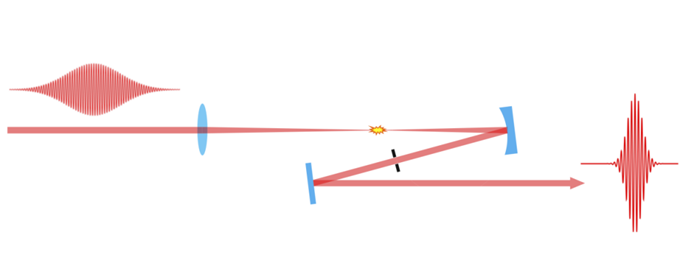
Figure 1: Schematic diagram of the experimental setup [1]

Near the focal point, the laser peak intensity surpasses the air ionization threshold, exciting a plasma spark. This plasma region introduces negative group velocity dispersion (GVD) in space, modulating the propagation speeds of the laser pulse's leading and trailing edges. As the positive dispersion from SPM and the negative dispersion from the plasma partially compensate each other during propagation, the pulse undergoes self-compression in free space.

The laser plasma generates a conical radiation structure in the air, with the conical edge containing blue-shifted pulses that have been temporally compressed. The researchers utilize a spatial aperture positioned about 250 mm from the focus to select the peripheral region of the cone, extracting the self-compressed pulses. As shown in Figure 2, the central wavelength of this pulse region is approximately 680 nm, exhibiting significant blue-shifting compared to the input pulse, with a spectral bandwidth extending to the 600–800 nm range.

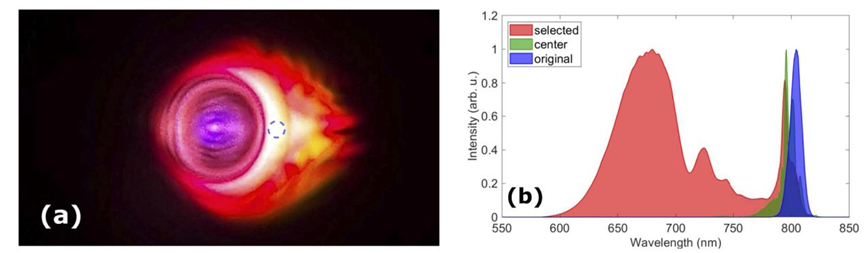
Figure 2: Self-compressed output spot and spectrum of laser-focused air conical radiation [1]

SHG-FROG measurements reveal that the pulse is compressed to 8.8 fs (FWHM), corresponding to a Fourier transform limit width of 5.1 fs, without the use of any dispersion compensation elements, as depicted in Figure 3. The spatially filtered compressed pulse possesses a single pulse energy of about 44 μJ and a conversion efficiency of 2.4%. This energy level satisfies the requirements of most typical ultrafast pump-probe and time-resolved nonlinear spectroscopy experiments.

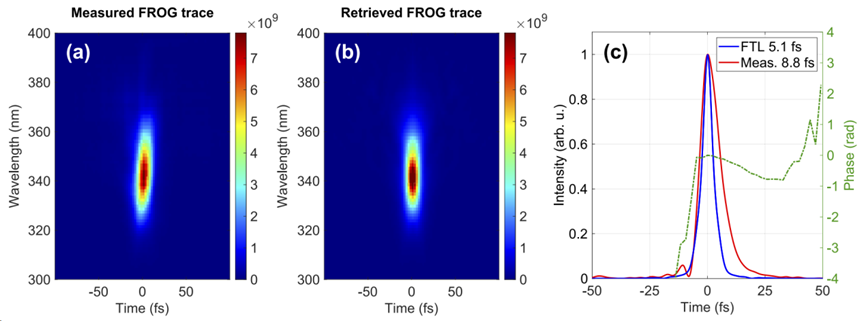
Figure 3: SHG-FROG measurement results demonstrating pulse compression to 8.8 fs [1]

To evaluate system stability, the experiment was continuously run for 1.2 hours, with pulse energy and pointing angle recorded every second. The root mean square (RMS) value of energy fluctuations was 1.1%. Beam drift was measured using far-field focal plane imaging, revealing 5.5 μrad in the horizontal direction and 5.0 μrad in the vertical direction. Overall, the system exhibited excellent output stability and pointing retention, as shown in Figure 4.

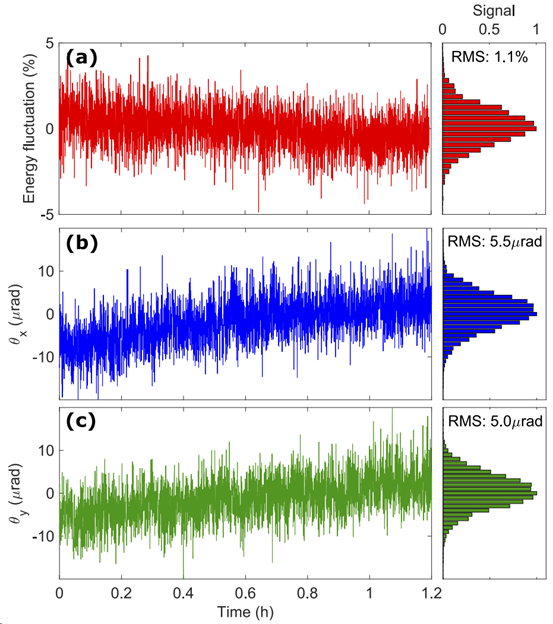
Figure 4: Fluctuation statistics of single pulse energy and beam pointing angle over 1.2 hours [1]

This method leverages the nonlinear response of air and the dispersion characteristics of plasma to achieve pulse self-compression without the need for additional nonlinear media or dispersion compensation elements. Compared to traditional hollow-core fiber solutions, it avoids the requirement for a vacuum system or high-precision gas control. Furthermore, unlike thin-glass compression solutions, it does not necessitate complex dispersion compensation structures, leading to a more compact device architecture.

It is important to note that this method's pulse compression relies on high incident peak power, and the energy extraction efficiency within the compression region is limited. Thus, it is currently more suited for medium-energy laser systems, particularly under experimental conditions that prioritize simplified compression structures and high device stability.

References:

[1] X. Xie, A. L. Cavalieri, and S. L. Johnson, "Self-compression of femtosecond laser pulses in ambient air through conical radiation," Opt. Lett. 48, 5101 (2023). https://doi.org/10.1364/OL.501319