Interpretation: The Future of AI Generation

Highlights

Systematic Analysis and Unified Perspective: A systematic analysis of Trajectory Distillation (TD) reveals its essence as a lossy compression process. This perspective explains why TD methods, while effective at preserving global structure, inevitably sacrifice fine details.

Innovative Hierarchical Distillation Framework: Re-examines the roles of trajectory and distribution distillation, proposing a novel Hierarchical Distillation (HD) framework. This framework synergistically leverages the strengths of both methods, first constructing structure and then optimizing details.

Discriminator Optimized for Detail Refinement: Designs an Adaptive Weighted Discriminator (AWD), a novel adversarial mechanism specifically tailored to optimize local flaws in high-quality generators, thereby significantly enhancing final generation quality.

Figure 1. Comparison of generation quality between a 50-step teacher SANA and our 1-step high-definition method. Our approach achieves quality comparable to multi-step teachers.

Problems Addressed

This paper aims to solve the issue of excessive inference latency in diffusion models, particularly in single-step or few-step generation scenarios. Existing acceleration methods primarily fall into two categories:

Trajectory-based Distillation (TD): These methods effectively preserve the global structure of generated content but sacrifice high-frequency details due to their 'lossy compression' nature, leading to reduced fidelity.

Distribution-based Distillation: These methods theoretically achieve higher fidelity but often suffer from mode collapse and training instability, especially with poor initial distributions. Our work aims to overcome the inherent limitations of both methods by combining their strengths to achieve high-fidelity, efficient single-step generation.

Proposed Solution

This paper introduces a two-stage framework called Hierarchical Distillation (HD), with the core idea of 'building the skeleton first, then filling in the details.'

Stage 1: Structured Initialization

Utilizes a trajectory-based distillation method (specifically MeanFlow) to 'inject' structural prior knowledge from a multi-step teacher model into the student model. The goal of this stage is not to generate final results but to provide the student model with a structurally sound, high-quality initial distribution close to the real data manifold. This effectively stabilizes the subsequent training process.

Stage 2: Distribution Optimization

Uses the pre-trained model from Stage 1 as a generator for fine-tuning via Distribution Matching (DM).

Adversarial training is introduced in this stage to recover high-frequency details lost in Stage 1 and avoid mode collapse.

To address the issue of traditional discriminators providing ineffective supervision signals when faced with high-quality generators, this paper designs an Adaptive Weighted Discriminator (AWD). AWD dynamically assigns weights to different spatial locations (tokens) on the feature map through an attention mechanism, enabling the discriminator to focus more on local flaws and provide more precise guidance for generator detail refinement.

Applied Technical Points

Trajectory Distillation (TD): Uses MeanFlow as the implementation for structured initialization in Stage 1.

Distribution Matching Distillation (DMD): Used for detail optimization in Stage 2, aiming to align the generated distribution with the real data distribution.

Adversarial Training: Introduced in Stage 2 to stabilize training and mitigate mode collapse.

Adaptive Weighted Discriminator (AWD): One of the core technologies proposed in this paper, dynamically weighting features through learnable query embeddings and an attention mechanism to focus on discriminating local artifacts.

Achieved Results

Our method achieves state-of-the-art (SOTA) performance across multiple tasks.

On the ImageNet 256×256 class-conditional generation task, our single-step model achieves an FID score of 2.26, leading not only among single-step models but also comparable to its 250-step teacher model (FID of 2.27).

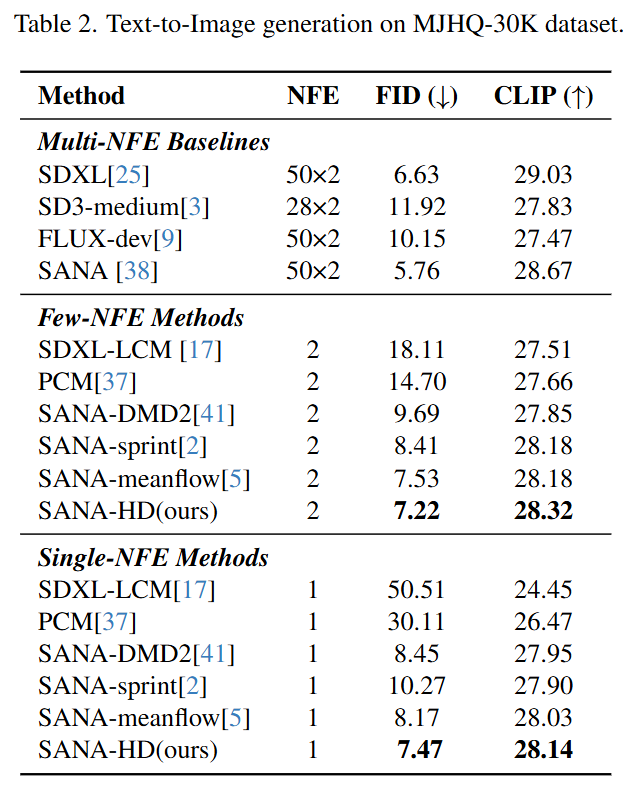
On the MJHQ-30K high-resolution text-to-image benchmark, both single-step and two-step models outperform existing distillation methods in terms of FID and CLIP scores, demonstrating strong generalization capabilities.

Methodology

This section introduces the technical details of the Hierarchical Distillation (HD) framework. First, a theoretical analysis unifies mainstream Trajectory Distillation (TD) methods, revealing their common limitations as motivation for our approach. Subsequently, the first stage of our pipeline is detailed, where MeanFlow-based TD injects strong structural priors into the student model. Finally, the second stage is described, where distribution matching is applied to optimize the well-initialized model for high-fidelity results.

Unified Perspective on Trajectory Distillation

This section conducts a theoretical analysis to clarify the modeling objectives of Trajectory Distillation (TD). Through mathematical derivation, it demonstrates that the objectives of several mainstream TD methods, including Consistency Models (CM/sCM) and Progressive Distillation (PGD), can be unified under a common framework of average velocity estimation. Based on this observation, a common limitation inherent to most TD methods is identified.

Proposition 1. Continuous Consistency Models implicitly model the average velocity over the interval [0, t].

Proof. The core principle of Consistency Models is to enforce network output consistency along any given PF-ODE trajectory. The differential form of this consistency constraint can be expressed as (detailed derivation in Appendix 6):

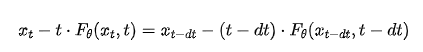
Where, in the limit dt → 0, this discrete relationship yields the differential form:

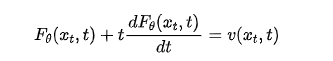
Recalling the relationship between instantaneous and average velocity in Equation (5). Specifically, for the interval starting from , it becomes:

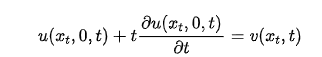
This reveals that as dt → 0, the CM network's output is implicitly trained to model the average velocity over the interval , i.e., .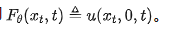

Proposition 2. As the number of distillation steps approaches infinity, Progressive Distillation (PGD) converges to modeling the average velocity over the entire interval .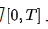

Proof. Progressive Distillation (PGD) is an iterative process that distills an N-step teacher model into a 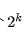-step student model over N rounds. In each round k, the student model 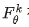is trained to predict the average of its teacher model's (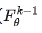) outputs at two consecutive time steps.

After N rounds of distillation, the output of the final single-step student model 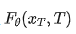can be expressed as the arithmetic mean of the original multi-step teacher model's outputs over 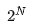discrete time steps (detailed derivation in Appendix 6):

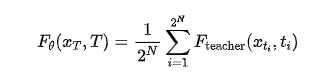
Where 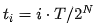represents discrete time steps. The original teacher model 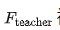is trained to approximate instantaneous velocity, i.e., 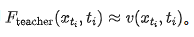. When the number of distillation rounds 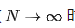, the sum converges to an integral:

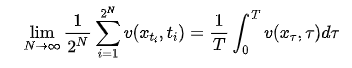
By definition, the right-hand side of Equation (13) represents the average velocity over the entire interval . This indicates that PGD also implicitly attempts to model average velocity.

Impact of Unified Perspective. The unified analysis yields two key insights that form the theoretical basis of our proposed method. (1) Our proof reveals that mainstream TD methods, regardless of their specific formulations, share a common essence: they train a single neural network to approximate a dynamic average velocity function . As an integral over a trajectory segment, this average velocity function encapsulates rich high-frequency dynamic information from the multi-step teacher model's PF-ODE path. Forcing a finite-capacity student model to perfectly replicate a complex function in a single step introduces a fundamental bottleneck from an information theory perspective. This provides a theoretical explanation for why all single-step TD methods inevitably suffer from fine-grained detail loss. We provide further empirical validation for this claim in Section 5.1. (2) Since all TD methods share the fundamental objective of modeling average velocity, we select MeanFlow as their representative implementation. This decision is based not only on its state-of-the-art performance but also, more importantly, on MeanFlow's explicit and direct modeling of average velocity, providing a mathematically elegant and robust implementation.

Stage 1: Structured Initialization via TD

As mentioned earlier, applying Distribution Matching Distillation (DMD) from scratch for single-step generation faces issues of training instability and mode collapse. A primary reason is the lack of overlap between the generated and real data distributions. To address this, we introduce a structured initialization stage. Trajectory Distillation (TD) is utilized to effectively inject the rich structural priors accumulated by the multi-step teacher model into the student model. This ensures that before the distribution matching stage begins, the student model already possesses strong capabilities to capture the macrostructure and layout of the target distribution. Based on the preceding analysis, MeanFlow is adopted as the distillation target for our TD stage. Although MeanFlow was originally proposed for training models from scratch, we argue that repurposing it as a distillation framework provides a learning signal with lower variance. When training from scratch, the model learns from random pairings of data and noise, where each sample presents a unique, high-variance target. In contrast, distillation leverages a pre-trained teacher model that has converged to a fixed, deterministic mapping from noise to data. This guidance from the teacher ensures consistent learning objectives throughout training, reducing the variance of gradient signals and leading to a more stable and efficient initialization stage.

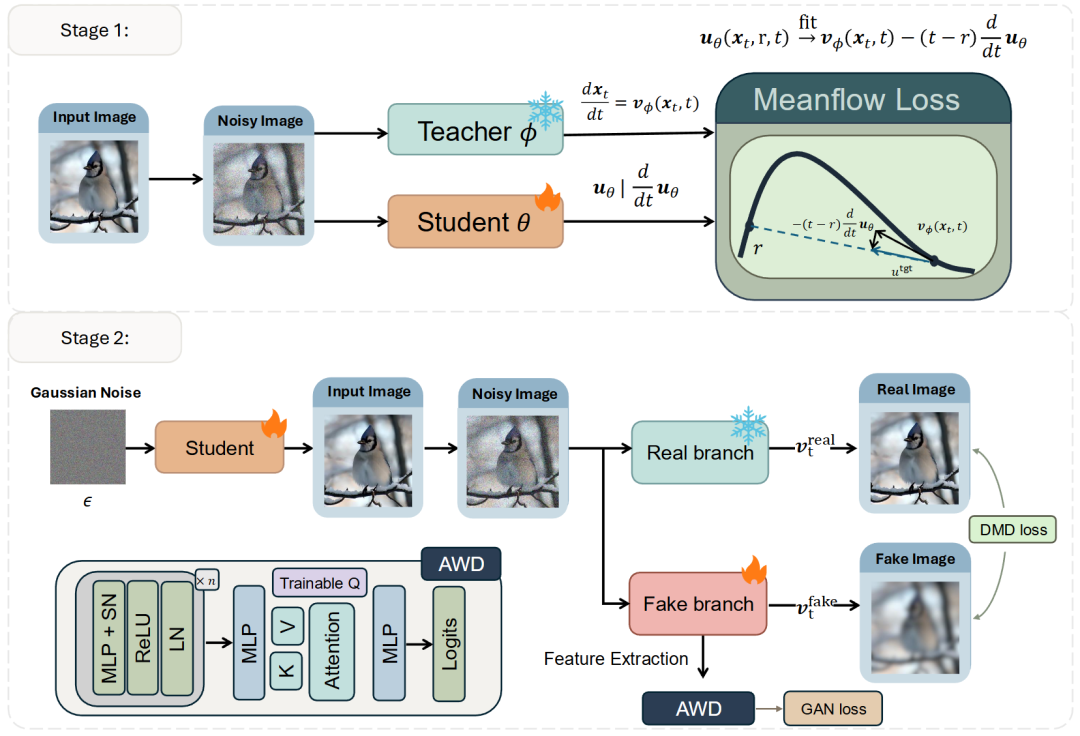Fig. 2. Hierarchical Distillation (HD) Pipeline. Our method consists of two main phases: (1) Structured Initialization: The MeanFlow-based approach instills foundational structural information into the student. (2) Distribution Refinement: The second phase employs an Adaptive Weighted Discriminator (AWD) designed specifically for the HD framework to recover high-frequency details. "SN" and "LN" denote Spectral Normalization [22] and Layer Normalization, respectively.

The flowchart for this phase is illustrated in the upper part of Fig. 2. Within our distillation framework, the true instantaneous velocity field (initially derived via linear interpolation in standard MeanFlow) is replaced with the output of a pre-trained teacher model. This directly guides the student to learn the teacher's trajectory dynamics. Specifically, we utilize classifier-free guidance (CFG) on the teacher model to define the instantaneous velocity field:

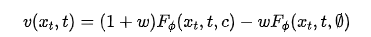
where 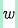represents the guidance scale, and denote conditional and unconditional inputs, respectively. By substituting this teacher-defined velocity field into MeanFlow's training objective (Equation (6)), we construct our distillation loss. The output of this phase is a student generator endowed with the teacher's structural priors. Although its fidelity with minimal steps is imperfect, it provides a well-posed initialization for subsequent distribution matching and refinement.

Phase 2: Distribution Optimization

After initialization through the Phase 1 model, the generator proceeds to Phase 2 for distribution optimization, recovering high-frequency details inherently lost when learning solely from teacher trajectories. We employ a DMD-based strategy to align the single-step output distribution of with the true data distribution. Since 's initial distribution already occupies a favorable region on the data manifold with significant overlap with the true distribution, DMD's training process becomes more stable and efficient. Its primary task shifts from "blind exploration" to "targeted refinement of details." For the score network in DMD, although the MeanFlow student model itself can predict instantaneous velocities, we still use the pre-trained teacher model to initialize both real and fake score branches. This prevents potential error accumulation and provides more accurate velocity field estimations. The loss function is presented in Equation (8).

To further stabilize training and mitigate the risk of mode collapse, an adversarial training strategy is introduced. We introduce a discriminator D that operates not in the high-dimensional pixel space but within the feature space of the teacher model, following the approach of [29]. The total adversarial loss comprises generator and discriminator losses, denoted as , : 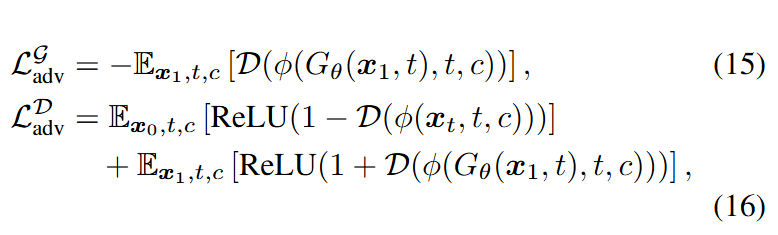where represents the feature extraction function, which takes an image, time, and condition as inputs and returns intermediate features from the teacher model. Here, denotes a noisy real image, while represents a generated sample.

Ultimately, the total loss formula is:

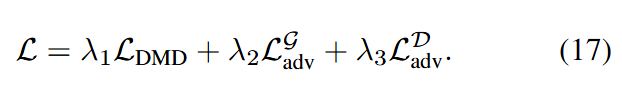
Adaptive Weighted Discriminator. Following TD initialization, the student model has already captured the overall structure of the target distribution. Imperfections are no longer global but manifest as subtle, localized artifacts. This renders traditional discriminators, which rely on global average pooling (GAP), largely ineffective. To address this challenge, we design the Adaptive Weighted Discriminator (AWD), as depicted in the bottom part of Fig. 2. Instead of assigning uniform weights to all tokens, our discriminator employs a learnable query embedding and an attention mechanism to dynamically weight different tokens on the feature map. Consequently, the discriminator can focus on local regions most likely to contain artifacts, providing the generator with more precise and effective gradients.

The final student model trained through this hierarchical framework is capable of generating images comparable in quality to multi-step teacher models with minimal steps while preserving diversity.

Experiments

The experimental section first validates its core theoretical hypothesis through a two-dimensional toy experiment: Trajectory Distillation (TD) exhibits an information bottleneck, with its performance ceiling constrained by the student model's capacity. Experiments demonstrate that increasing model capacity significantly enhances the single-step student model's performance. However, even with a 50-fold increase in capacity, it cannot perfectly replicate the teacher model's multi-step trajectories, proving that TD alone is insufficient for optimal single-step generation quality and necessitating a subsequent optimization phase.

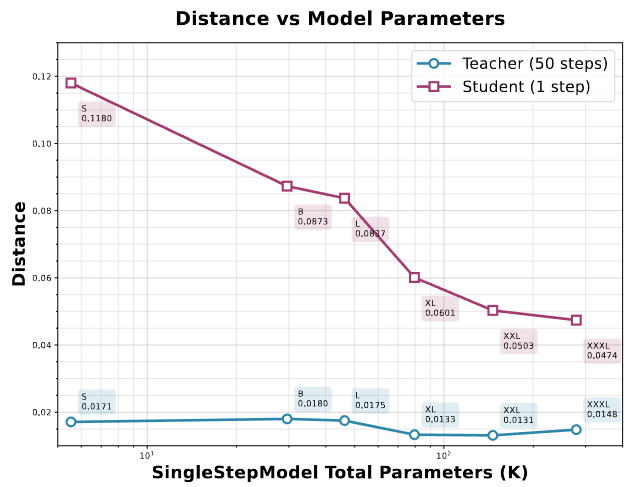Fig. 3. Relationship between Trajectory Distillation (TD) Performance and Model Size. The upper limit of TD performance increases with the number of model parameters.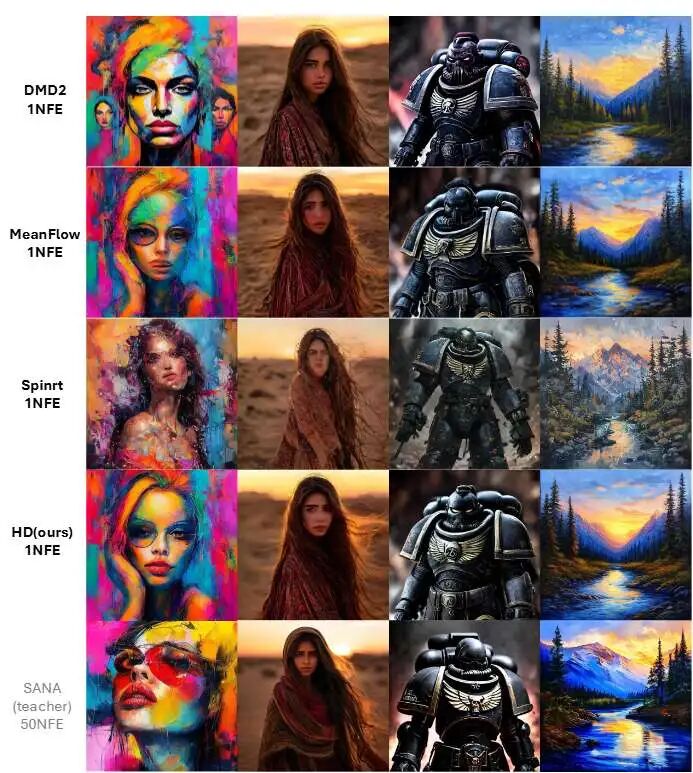

In the primary comparative experiments, this paper validates the effectiveness of the HD framework on two benchmarks: ImageNet 256×256 and Text-to-Image (MJHQ-30K).

On ImageNet, the HD single-step model achieves an FID of 2.26, outperforming all other single-step methods (e.g., MeanFlow's 3.43, DMD's 6.63) and nearly matching the 250-step teacher model (FID 2.27). This represents a substantial inference acceleration (approximately 70-fold) with minimal performance loss.

In the Text-to-Image task, HD surpasses existing methods, including SDXL-LCM, DMD2, and MeanFlow, in terms of both FID and CLIP scores under single-step and two-step settings, demonstrating its universality and superior performance.

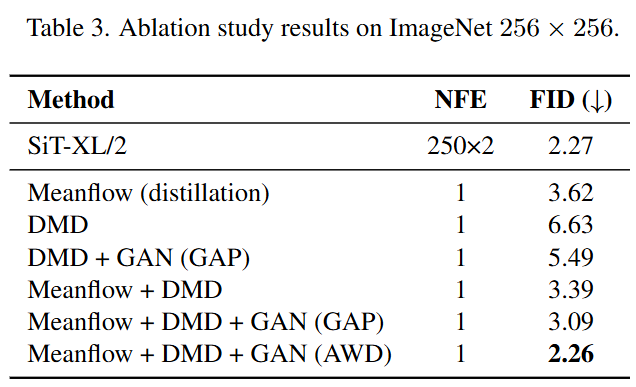
Ablation experiments further dissect the contributions of each component within the HD framework. The results indicate:

TD Initialization is Crucial: Compared to models without TD initialization, TD-initialized models exhibit significant performance improvements (FID reduced from 5.49 to 3.09), confirming that providing a high-quality structural prior is key to success.

Effectiveness of AWD: Compared to discriminators using standard Global Average Pooling (GAP), our proposed Adaptive Weighted Discriminator (AWD) further reduces FID from 3.09 to 2.26, demonstrating AWD's superiority in focusing on local flaws and guiding model refinement of details.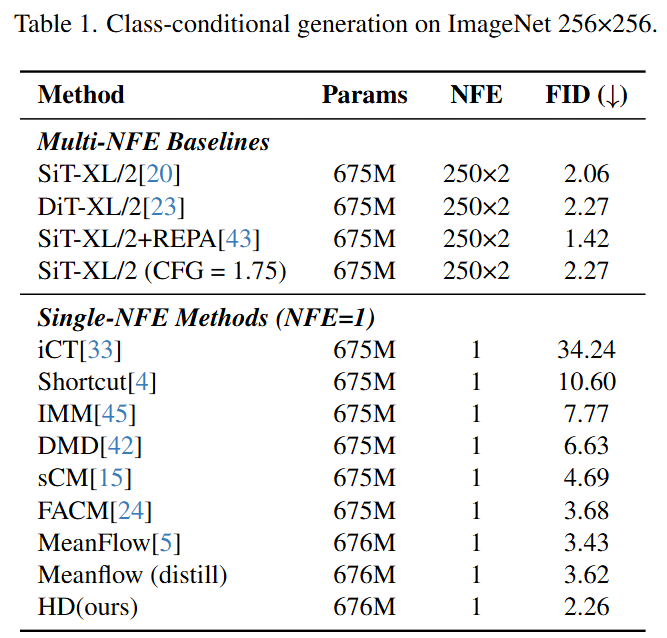

Conclusion

This work presents a unified theoretical formulation for Trajectory Distillation (TD), identifying a common "average velocity" modeling objective that leads to an information-theoretic bottleneck. This analysis reveals why TD excels at global structure but fundamentally struggles with fine details. Inspired by this, we propose a novel Hierarchical Distillation (HD) framework that synergistically combines TD and distribution matching. Our approach first leverages TD as a powerful initializer, injecting rich structural priors from the teacher model to establish a well-posed starting point for the student model. Subsequently, this robust initial model is refined through distribution matching. To enhance this phase, we introduce a tailored adversarial training process equipped with our proposed Adaptive Weighted Discriminator (AWD). By dynamically focusing on local artifacts of the well-initialized model, it provides more precise guidance for detail refinement. Extensive experiments demonstrate that our single-step student model significantly outperforms existing distillation methods and achieves fidelity comparable to its multi-step teacher model. By diagnosing and overcoming TD's bottleneck, this work provides an effective new paradigm for few-step or even single-step high-fidelity generation.

References

[1] From Structure to Detail: Hierarchical Distillation for Efficient Diffusion Model