Insight: The Future of AI-Generated Content

Key Highlights

HyperAlign, a pioneering framework, dynamically adjusts denoising processes through a hypernetwork, ensuring test-time alignment for diffusion models. This results in generated images that seamlessly blend user-intended semantics with visual allure.

We've engineered diverse adaptive weight generation strategies, enhancing alignment efficiency and flexibility. Beyond traditional reward scores, we've introduced preference regularization to mitigate reward hacking risks.

Our method's prowess was evaluated across leading generative models (e.g., SD V1.5 and FLUX). HyperAlign consistently outperformed baseline models and other fine-tuning/test-time scaling techniques, showcasing its superiority and effectiveness.

Summary Overview

Addressed Challenges

Mismatch between diffusion model outputs and user preferences/intentions: Generated images often fall short in aesthetic quality and semantic alignment with prompts.

Limitations of Existing Alignment Methods:

• Fine-tuning Approaches: Prone to reward over-optimization, leading to a loss of diversity.
• Test-time Scaling Methods: High computational demands, susceptibility to reward under-optimization, and inadequate alignment.

Proposed Solution

Introducing the HyperAlign framework, which achieves efficient and effective test-time alignment through hypernetwork training:

• Core Idea: Instead of directly modifying latent states, dynamically generate low-rank adaptation weights (LoRA) via a hypernetwork to modulate the diffusion model's generative operators, thereby adaptively refining denoising paths.
• Variant Designs: Developed three strategies (step-by-step, starting point, segmented generation) based on hypernetwork application frequency to balance performance and efficiency.
• Optimization Objective: Utilized reward scores as training targets and incorporated preference data for regularization to counteract reward hacking.

Applied Technologies

• Hypernetwork Architecture: Accepts latent variables, timesteps, and prompts as inputs; outputs dynamic modulation parameters (LoRA weights).
• Low-Rank Adaptation (LoRA): Reduces parameter count, avoiding the high costs associated with generating full model weights.
• Reward-Conditioned Alignment: Optimizes generative trajectories based on reward scores and incorporates preference data regularization.
• Multi-Paradigm Adaptation: Implemented across diverse generative paradigms, including diffusion models (e.g., Stable Diffusion) and rectified flows (e.g., FLUX).

Achieved Results

• Significant Performance Improvement: Outperformed existing fine-tuning and test-time scaling baselines in enhancing semantic consistency and visual appeal.
• Efficient Alignment: Eliminated the high computational costs of traditional test-time methods through dynamic weight generation, enabling efficient real-time adjustments.
• Balanced Diversity and Alignment: Mitigated reward over-optimization via regularization, maintaining generative diversity while aligning more closely with human preferences.
• Broad Applicability: Successfully applied to multiple advanced generative models, validating the framework's versatility and scalability.

Diffusion Model Alignment

Preliminary Knowledge of Score-Based Generative Models

Diffusion models capture data distributions by learning to reverse a progressive noise addition process applied to clean data. Given a data distribution, the forward process of a diffusion model follows a stochastic differential equation (SDE) under specific conditions, gradually perturbing clean samples with Gaussian noise until they resemble Gaussian noise:

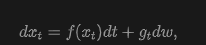
where denotes the standard Wiener process, and and represent the drift and diffusion coefficients, respectively.

By reversing this process from , a data generation process via inverse SDE can be obtained:

where denotes the marginal distribution of at time . The score function can be estimated by training a model :

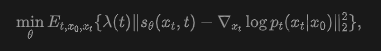
where is a weight function, is the Gaussian transition density, and . The approximated defines a learned distribution .

Score-based models unify diffusion models and flow matching models, where sample trajectories of are generated via stochastic or ordinary differential equations (SDEs or ODEs). For clarity and brevity, subsequent descriptions will primarily focus on diffusion models without loss of generality. The analyses and methods presented herein naturally extend to both diffusion and flow matching models under this unified formulation.

Reward-Based Diffusion Model Alignment

Conditional Diffusion Models and Score Functions: This work considers conditional diffusion models that learn distributions , where denotes conditional variables. The training objective is to generate samples via inverse diffusion, denoising sampled noise under the control of condition . In image generation, represents input prompts, guiding user instructions for generated content. For discussion, this work adopts discrete score-based models under variance-preserving settings, with sampling formulas:

where , , , and is a linearly increasing noise scheduler. This iterative denoising process forms a trajectory in latent space, gradually transforming noise into clean samples reflecting input prompts .

Reward-Based Diffusion Model Alignment: Although existing text-to-image (T2I) models demonstrate strong generative capabilities, results often fall short of user expectations, exhibiting poor visual appeal and semantic inconsistencies with input prompts. This limitation arises because score functions are learned from large-scale uncurated datasets that deviate from human preference distributions. To bridge this gap, diffusion model alignment is introduced to enhance consistency between generated images and human user preferences.

Leveraging human preference data, a reward model capturing human preferences (e.g., aesthetic preferences) can be obtained. By associating with condition , the reward model can be expressed as , assuming it partially captures consistency between and as well as visual aesthetic preferences. It can be explicitly learned from preference data or implicitly modeled via direct data utilization. Given a learned and a reward model, diffusion model alignment can be formulated as solving for a new distribution:

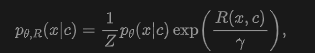
where is the KL regularization coefficient, balancing reward maximization and base model consistency. Training-based alignment approaches via reinforcement learning (RL) and direct backpropagation optimize target rewards. While effective, these methods typically incur substantial computational overhead and risk over-optimization, reducing generative diversity. In contrast, test-time scaling methods modify temporal states using guidance to achieve alignment objectives. Since the generative distribution manifests as trajectories of during sampling, test-time alignment can be viewed as guiding these trajectories to better match desired conditional distributions .

Methodology

This work aims to train a hypernetwork to achieve efficient and effective test-time alignment for diffusion models, termed HyperAlign.

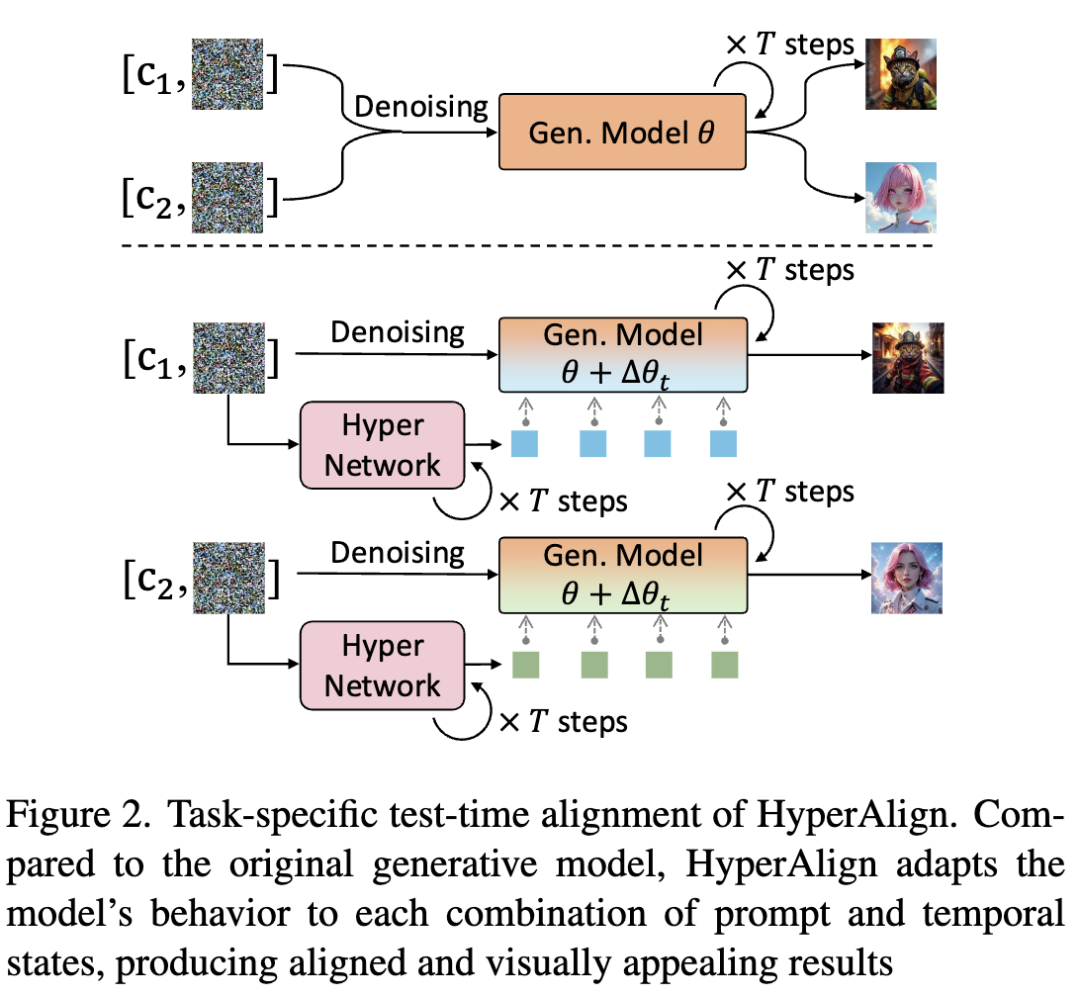Task-Specific Test-Time Alignment with HyperAlign

Test-Time Diffusion Alignment via Guidance

Test-time diffusion alignment methods adjust generative trajectories to better satisfy alignment objectives. Existing test-time computational strategies can be broadly categorized into noise sampling approaches and gradient-based diffusion guidance methods.

• Noise Sampling Methods: Attempt to identify favorable noise candidates based on reward feedback. However, exploring the vast high-dimensional noise space is computationally expensive and difficult to converge, resulting in inefficiency and suboptimal outcomes.
• Gradient-Based Diffusion Guidance: Directly computes gradients from specific objectives and utilizes them to guide denoising trajectories by modifying temporal states.

To effectively align diffusion models by directly injecting guidance from rewards, this work trains a hypernetwork that generates prompt-specific and state-aware adjustments at each denoising step. This design maintains computational efficiency by amortizing expensive test-time optimization into a compact, learnable modeling process during fine-tuning.

Before introducing our method, we first analyze diffusion guidance approaches that leverage generative gradients to guide denoising trajectories. Based on Bayesian rules, an approximate expression for can be derived, where the first term corresponds to the unconditional score, requiring no additional optimization. Thus, this work focuses on the second term, injecting reward gradients into the denoising process:

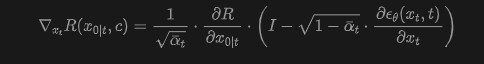
where the reward function is practically applied to the decoded image domain via a decoder. For brevity, the decoder symbol is omitted here. By substituting the above into the diffusion update formula, it can be observed that guidance-based methods achieve alignment by injecting perception-aware reward diffusion dynamics into , essentially altering the transition path from to .

Hypernetwork for Test-Time Alignment

Gradient guidance methods perform test-time alignment by directly modifying temporal states using scores derived from rewards, thereby adjusting denoising trajectories. However, backpropagating gradients from reward models to generators incurs significant computational overhead, reduces inference speed, and remains disjoint from the generator's training process.

To mitigate these issues while retaining task-specific modeling advantages, this work trains a hypernetwork that effectively guides generative trajectories based on tasks, inputs, and current generative states. Its test-time alignment capability is learned during training by injecting reward-based guidance into the hypernetwork. Unlike fine-tuning alignment methods that adapt to all user intention combinations using a fixed parameter set, our approach is prompt-specific and state-aware, dynamically generating adaptive modulation parameters at each denoising step to align generative trajectories.

Hypernetwork as a Dynamic LoRA Predictor: Our goal is to learn a hypernetwork that takes and as inputs and outputs adjustments for each step of the generative process. A naive approach would involve learning an alignment score to replace Equation (6), but this requires a formula similar to the original generative score, resulting in high complexity. Instead, we design the hypernetwork to directly adjust the score corresponding to network parameters in the original generative model, specifically by generating a lightweight low-rank adapter (LoRA) for .

As shown in Figure 3, the hypernetwork architecture primarily consists of two components: a Perception Encoder and a Transformer Decoder.

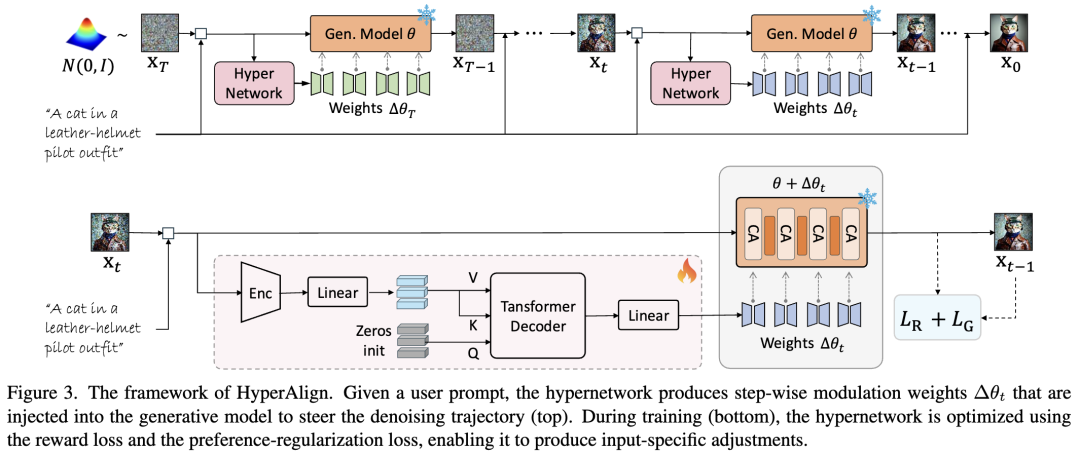
Input Processing: Specifically, the input time latent variable , timestep , and prompt are first fed into the Perception Encoder, which comprises downsampling blocks from a pretrained U-Net used in generative model pretraining. The pretrained U-Net carries rich diffusion priors, making it a natural encoder for capturing semantic representations across diverse input combinations.

Feature Decoding and Generation: Encoded features are subsequently projected through a linear layer and passed to the Transformer Decoder. Here, zero-initialized tokens generate Queries (Q), while encoded features generate Keys (K) and Values (V). The Transformer Decoder integrates temporal and semantic information via cross-attention mechanisms.

LoRA Output: A subsequent linear layer maps the decoded features to LoRA weights:

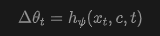
where denotes the parameters of hypernetwork . Temporally, the generated LoRA weights are integrated into the original model parameters, yielding an input- and step-specific score function (abusing notation to denote integration), thereby modifying the underlying denoising trajectory.

Efficient HyperAlign (Efficient HyperAlign): By default, the hypernetwork design in Equation (7) can be adaptively applied to all generative steps starting from the initial step (termed HyperAlign-S). To balance inference efficiency, this work further develops two variants:

• HyperAlign-I: Trained to predict LoRA weights only once at the starting point, i.e., , and use them for all steps.

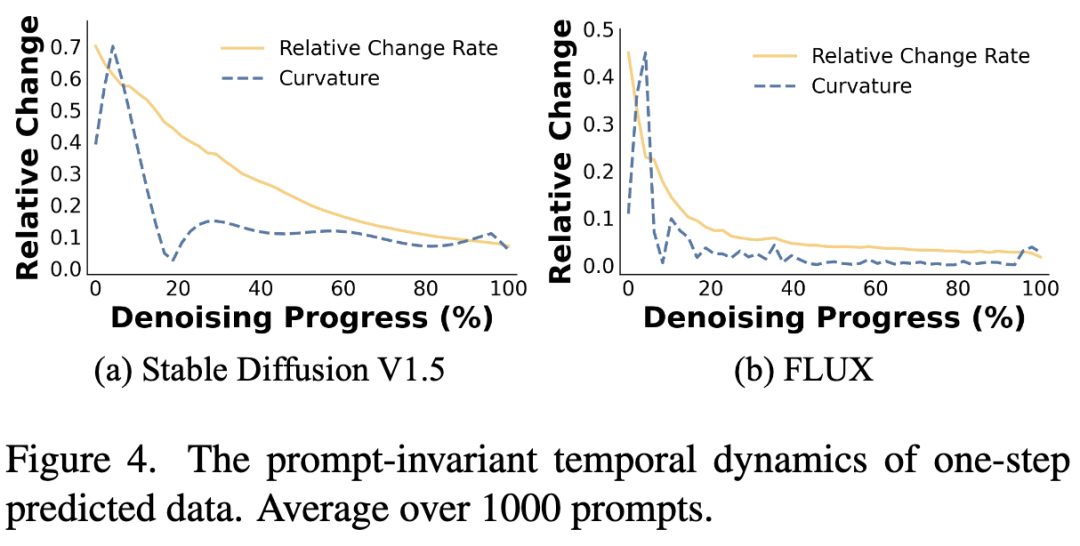
Segmented Variant (HyperAlign-P): This variant generates new weights at several crucial time steps, with all time steps within the same segment sharing identical LoRA weights. As illustrated in Figure 4 below, this study calculates the relative distance between latent variables predicted in a single step. Smaller values suggest that adjacent latent variables are similar to one another. The findings support the grouping of similar latent variable states into segments and the sharing of the same LoRA weights, which aligns with the diffusion behavior across different denoising stages. This study calculates the curvature rate to pinpoint key points that exert a greater influence on the trajectory. The hypernetwork is trained to regenerate LoRA weights solely at these key steps, enabling adaptive modulation of the diffusion process with less computation than HyperAlign-S, thereby achieving a balance between efficiency and performance.

HyperAlign Training

To optimize the hypernetwork, reward scores can serve as the training objective. By maximizing the reward signal, the model is incentivized to generate intermediate predictions with a higher conditional likelihood, thereby aligning the latent variable trajectory with the true conditional distribution:

Regularization for Reward Optimization: While maximizing the reward objective encourages the model to produce high-reward, conditionally aligned latent variable states, it also presents two key challenges:

Inaccurate reward signals stemming from the ambiguity of one-step predictions in early denoising stages; and the risk of over-optimization, where aggressive reward maximization leads to 'reward hacking' or a decline in visual fidelity.

To address these issues, this study introduces a regularization loss to constrain the alignment process and maintain generation quality:

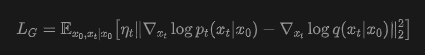
Where represents a hyperparameter, is sampled from preference data , and . This encourages the learned denoising conditional scores to align with those in the preference data, thereby mitigating the reward hacking problem.

The final learning objective for hypernetwork optimization is as follows:

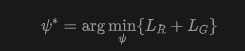
This method is not confined to diffusion models; as previously stated, HyperAlign is equally compatible with flow-matching models (e.g., FLUX in the experiments).

Experimental Results

Experimental Setup

Models and Data: SD V1.5 and FLUX were employed as the base models. HPSv2 served as the reward model. Preference data for the regularization loss was sourced from Pick-a-Pic and HPD.

Datasets and Metrics: The evaluation datasets encompassed Pick-a-Pic, GenEval, HPD, and Partiprompt. Six AI feedback models—PickScore, ImageReward (IR), HPSv2, CLIP, GenEval Scorer, and Aesthetic Predictor—were utilized to assess image quality, prompt alignment, and visual aesthetics.

Comparison with Existing Methods

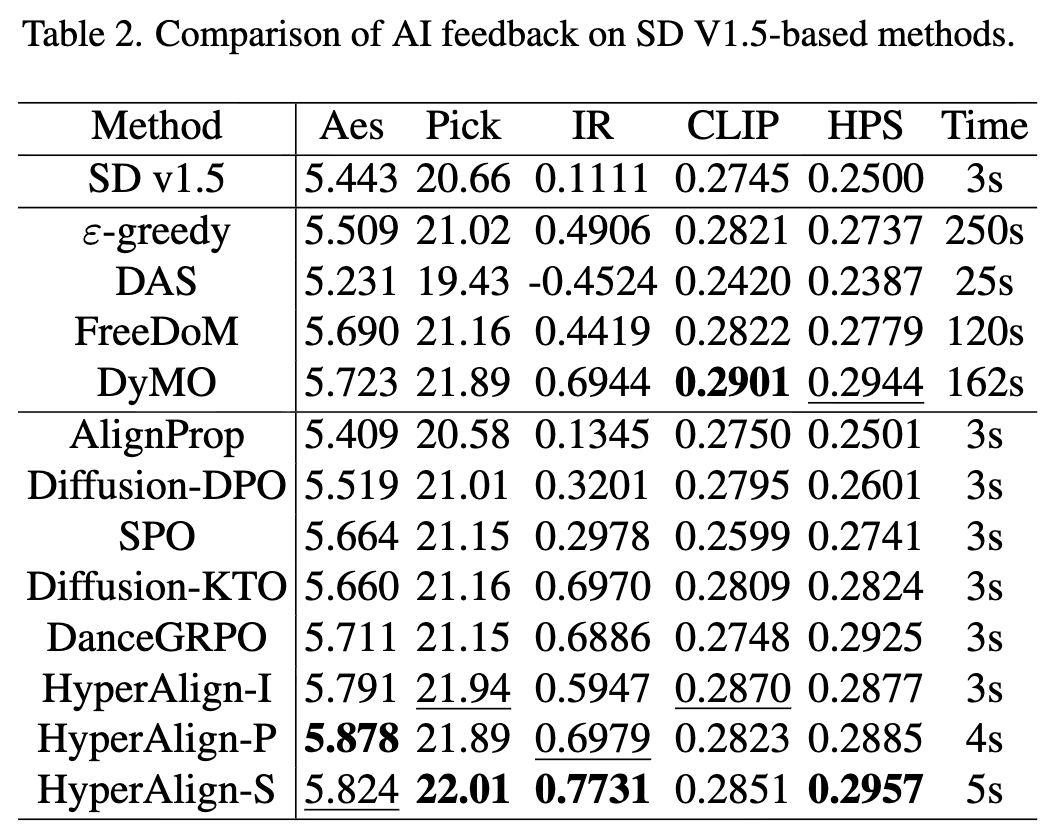
This study compared HyperAlign with fine-tuning methods (e.g., DPO, KTO, GRPO) and test-time scaling methods (e.g., BoN, -greedy, FreeDoM, DyMO).

Quantitative Analysis (as shown in Tables 1 and 2 below):

On the FLUX and SD V1.5 base models, HyperAlign outperformed existing fine-tuning and test-time scaling baselines across multiple metrics (Pick, IR, CLIP, HPS).

HyperAlign effectively achieved alignment, with HyperAlign-S (per-step adjustment) performing optimally, while HyperAlign-I (initial step only) and HyperAlign-P (segmented steps) offered faster inference speeds while remaining competitive.

In contrast, test-time methods often suffered from insufficient optimization, while fine-tuning methods yielded suboptimal results due to a lack of input adaptability.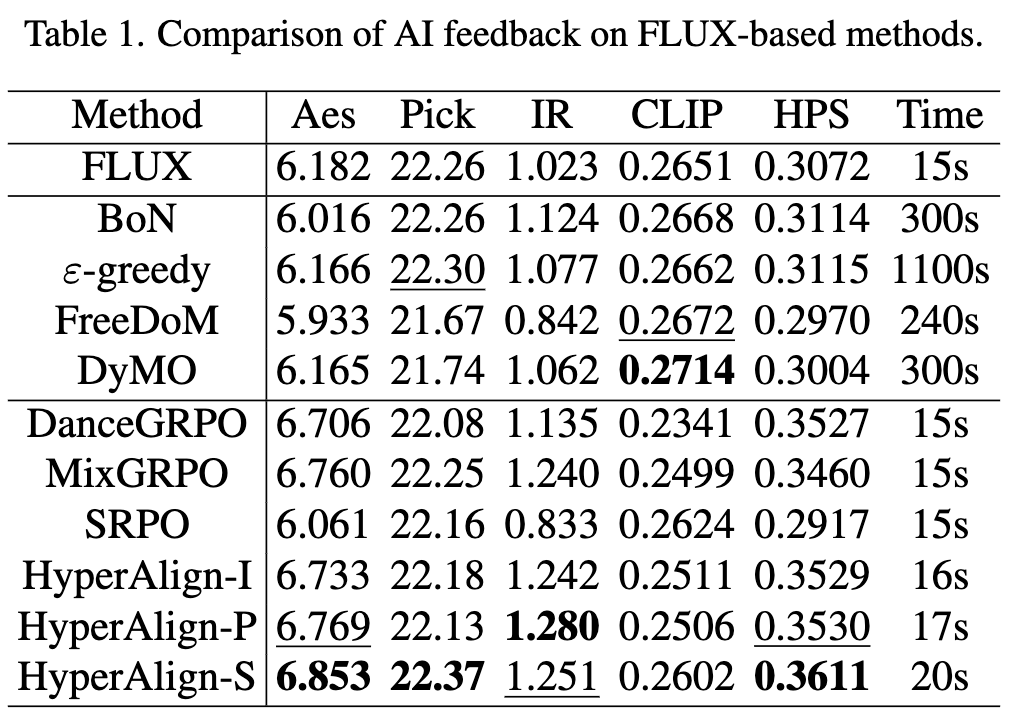

Qualitative Assessment (as shown in Figures 5 and 6 below):

Visual comparisons revealed that HyperAlign generated images with coherent layouts, rich semantics, and superior visual aesthetics. Test-time alignment methods produced unstable results with noticeable artifacts; fine-tuning methods, while scoring higher, often over-optimized, resulting in oversaturated colors or distortions.

Inference Efficiency:

HyperAlign generated single images in seconds (approximately 3-5 seconds on SD V1.5 and 16-20 seconds on FLUX), comparable to the base models. In contrast, test-time scaling methods (e.g., -greedy) incurred significant time costs (hundreds of seconds) due to gradient computations or repeated sampling. The additional time cost for HyperAlign to generate and load adaptive weights was negligible.

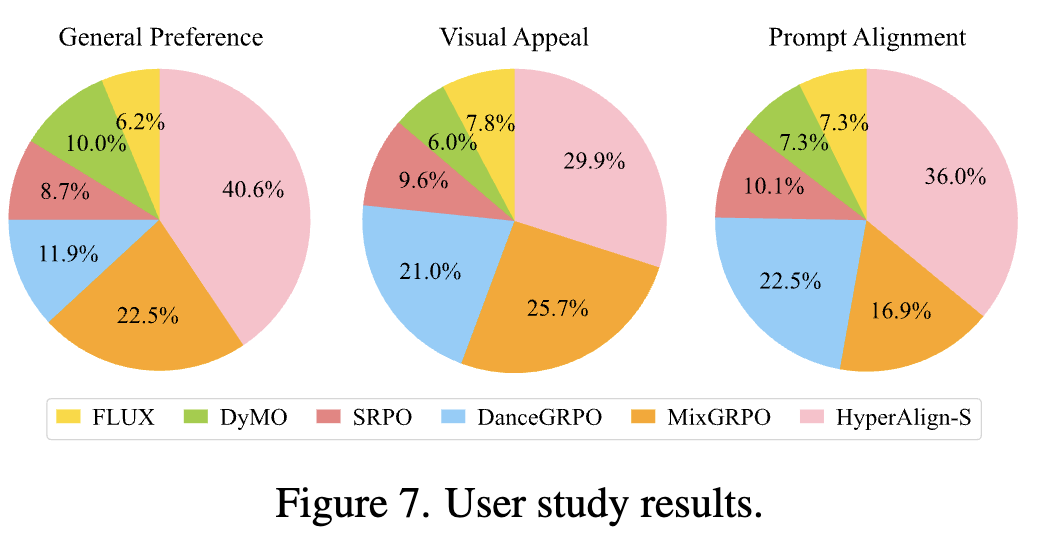
User Study (as shown in Figure 7 below):

In a user study targeting the FLUX model, 100 participants voted on three dimensions (overall preference, visual appeal, prompt alignment). HyperAlign-S achieved the highest user approval ratings across all dimensions, significantly outperforming methods such as DyMO, SRPO, and MixGRPO.

Ablation Study

Impact of Regularization Data: Utilizing HPD instead of Pick-a-Pic as regularization data, or incorporating PickScore as a reward, HyperAlign remained robust, demonstrating the method's strength (as shown in Table 3 below).

Role of Loss Functions: Fine-tuning with preference data alone yielded minimal gains; reward optimization alone led to over-optimization (e.g., oversaturated colors). Combining reward loss and regularization loss improved metrics while preserving visual naturalness (as shown in Figure 13 below).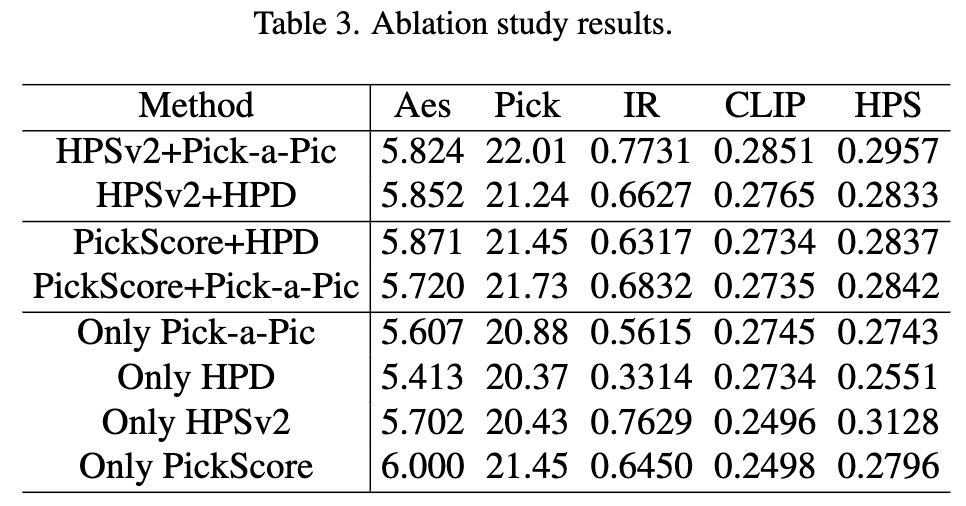

Additional Analysis

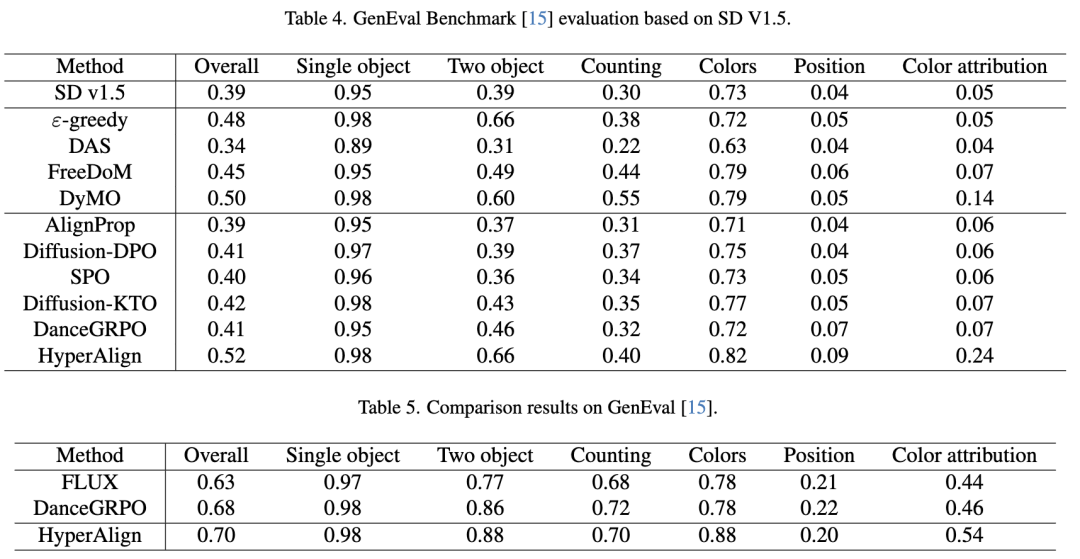
GenEval Benchmark: HyperAlign excelled in fine-grained metrics such as object synthesis and attribute binding (as shown in Tables 4 and 5 below).

LoRA Weight Dynamics: Analysis revealed that as the denoising process progressed, the cosine similarity between generated LoRA weights and initial weights decreased, while the change rate increased, indicating that different time steps served distinct functional roles (as shown in Figure 8 below).

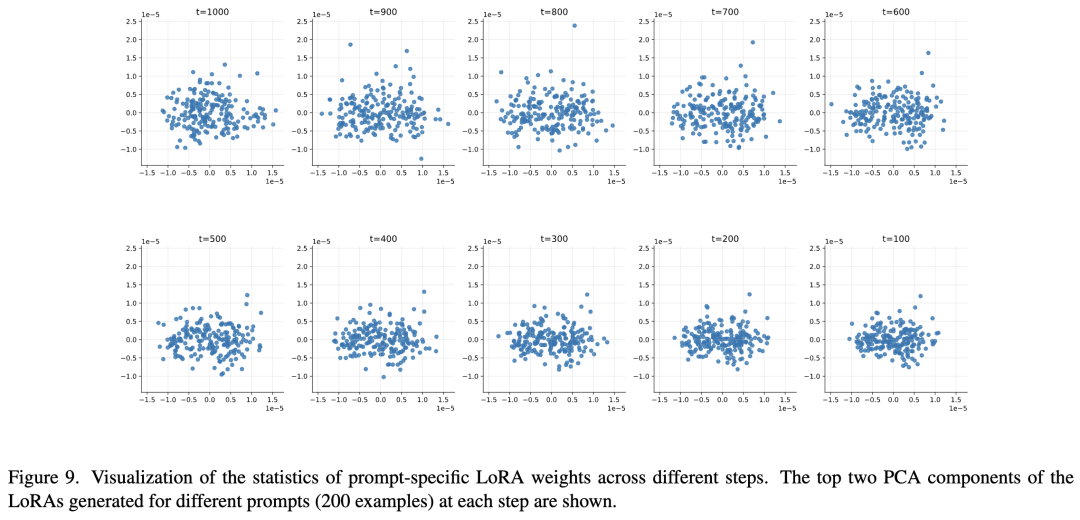
Diversity: PCA analysis demonstrated that HyperAlign generated unique LoRA weights for different prompts, particularly in the early generation stages (as shown in Figure 9 below).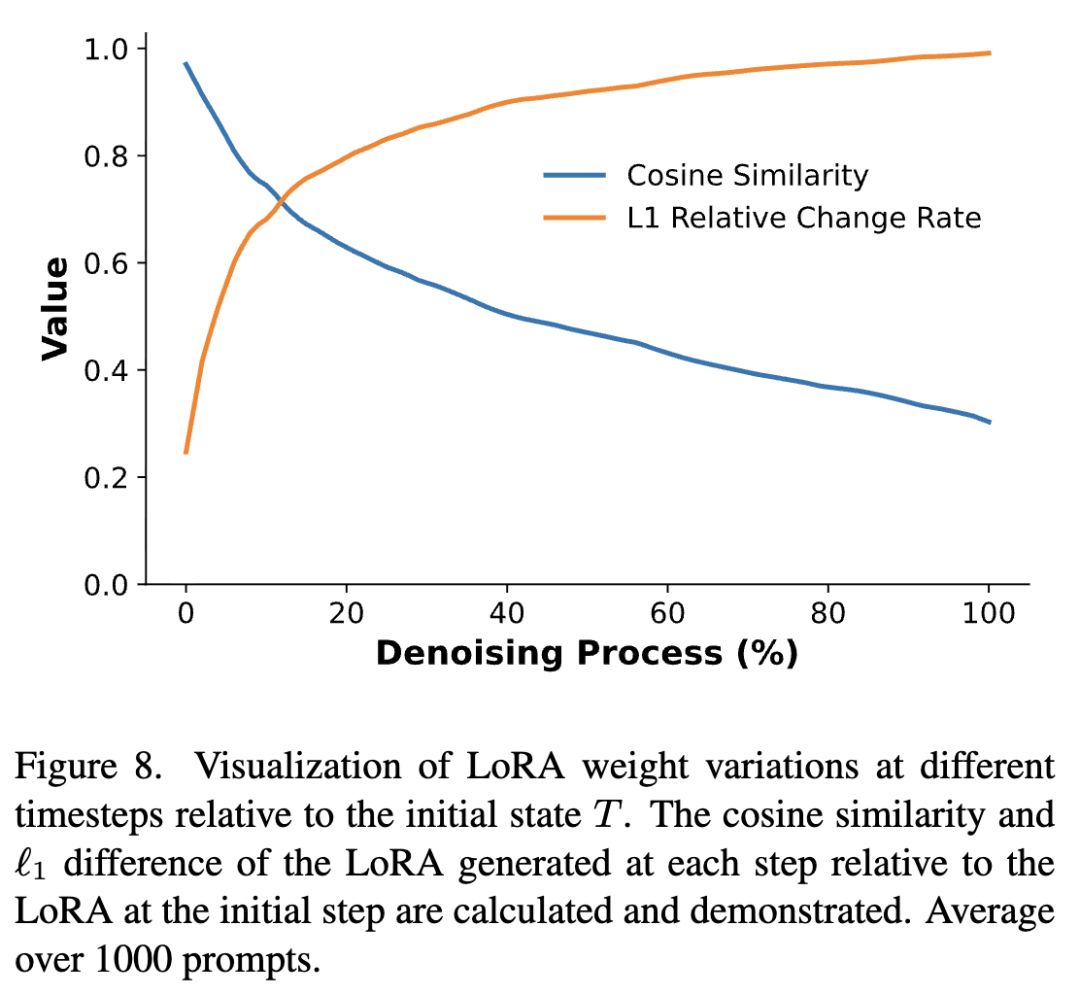

Conclusion

HyperAlign represents an efficient test-time alignment framework for generative models based on hypernetworks. HyperAlign achieves trajectory-level alignment via reward signals by dynamically generating low-rank modulation weights during denoising steps. Its variants offer flexible trade-offs between computational efficiency and alignment precision. Extensive experiments on diffusion models and rectified flow backbones demonstrate HyperAlign's superior performance in semantic consistency and aesthetic quality compared to existing fine-tuning and test-time alignment methods. Future work will focus on developing lighter hypernetwork designs while enhancing dynamic adaptability to further improve system efficiency and scalability.

References

[1] HyperAlign: Hypernetwork for Efficient Test-Time Alignment of Diffusion Models